引言

由于卷积核数据在计算过程中保持不变，更新较慢。这样就可以利用LUT来存储权重并同时进行乘法运算。LUT乘法器的实现很早就已经研究过，本论文正是在此基础上，提出了用于实现可配置的卷积实现方法。基于LUT的乘法器不会受到FPGA中DSP资源的限制，能够将神经网络加速应用于低端FPGA芯片。

LUT乘法器的实现

一个LUT有固定的输入和输出管脚，例如在xilinx的zynq系列器件中，LUT有5个输入1个输出或者4个输入两个输出。如何用LUT来实现任意大小的乘法运算呢？这里用到了一个基本的数学法则：因式分解。考虑一个补码数据x，其有Bi bit，那么表示为：

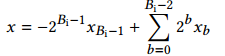
如果这个数被一个常数c乘，这个乘法可以被分解为更小bit的乘法，然后对这些小份乘法进行位移和求和。

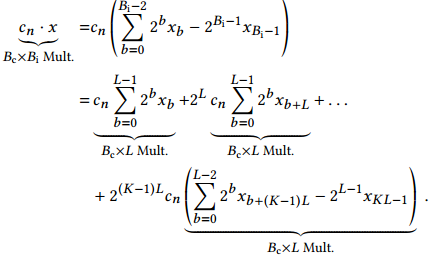
这样就将一个BcxBi bit的乘法分解成多个BcxL的乘法，而这个小的乘法就可以去利用LUT来实现。将L设置为LUT的输入引脚数量，可以直接将乘法映射到LUT上，并且对LUT资源利用效率最高。

Compressor加法树

上述乘法的分解造成了大量的加法，因此需要较大的加法树来完成各个乘法结果移位后的累加。基于Generalized parallel counters（GPC）充分利用了FPGA中的LUT资源以及进位链，可以更好的映射到LUT上，减少LUT使用的浪费。其主要特点就是在一个LUT中实现最多个全加器的运算，这样能保证进位链最短，LUT资源利用率最高。

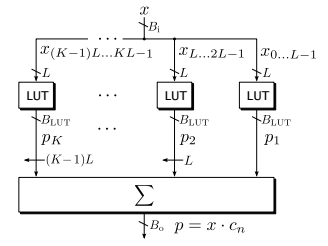
图2.1 乘法分解求和

可配置LUT

LUT是一个查找表，FPGA中对代码逻辑的映射都是映射到查找表中。现代的LUT有个特点就是可以进行动态配置，意味着可以在运行中去更新查找表的值。比如在xilinx的virtex，spartan和zynq器件中LUT就可以通过移位寄存器的方式来更新内部数据，32个时钟周期完成。这样就可以将卷积核数据存放在LUT中，然后在需要更新的时候进行更新。

可配置卷积的硬件架构

卷积运算的结构如图4.1所示，N个输入数据（x1, x2, .., xN）每个和c的乘法都被分解为K个乘法，然后将所有的部分乘法结果移位送入加法树。每个BcXL的乘法需要的LUT数量大致为Bc+L个。加法树输出的Bo位宽会远远大于输入位宽，因此需要进行rouding或者截位。

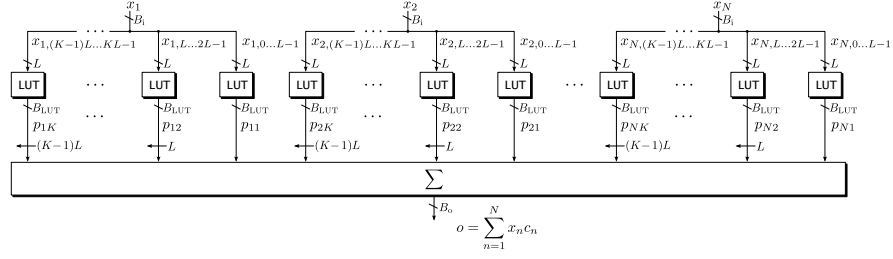
图4.1 基于LUT的卷积运算结构

论文中使用了LUT4输入2输出，使用4输入LUT而不是5输入是因为乘法分解的特点，4bit位宽对于16bit，8bit整型乘法来说更能充分利用LUT资源。这样N个输入数据的每个部分乘法总共花费的LUT数量就是：

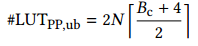
乘法和加法导致输出Bo位宽变大，需要减小位宽。论文采用了faithful rouding的办法。比如输入是12bit的数据，要求输出也要截位成12bit，如果在最后求和之后再进行截位，加法树中就因为计算多余位数求和而浪费LUT。如果每个乘法结果都截位为12，那么会造成最后结果精度较大丢失。如果先对每个乘法结果截位大于12bit的数据，根据总共求和的个数可以计算出需要保留的bit位数。这样就能够保证最后加法结果精度等于或者小于直接截位加法结果的精度。比如开始对每个乘法截位2^(-q-g)，因为总共有N*Bi/L个部分积结果。所以总共的精度损失为：

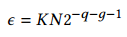
通过限制总精度损失在需要范围：

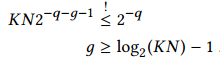
这样就可以得到g的数据。这样就能最大程度减少LUT的使用同时能保证良好精度。

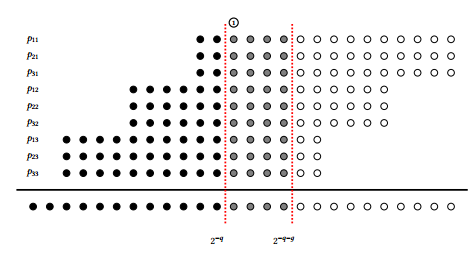
图4.2 3个输入x，bit位宽12bit，分解为4个乘法，输出要求12bit

现在来看如何对LUT进行数据的更新。由于将LUT用作4输入2输出，那么一个LUT可以计算出2bit结果的乘法。于是计算需要的每个个LUT的一部分用于和weights的偶数部分进行乘法，而另一部分用于和weights的奇数部分乘法。而LUT的配置接口只有一个CDI，因此就需要分别对LUT的这两部分进行配置。论文中先计算对应奇数部分weights的乘法结果，存储到LUT中，然后计算对应偶数部分weihts的乘法，存储到LUT中。

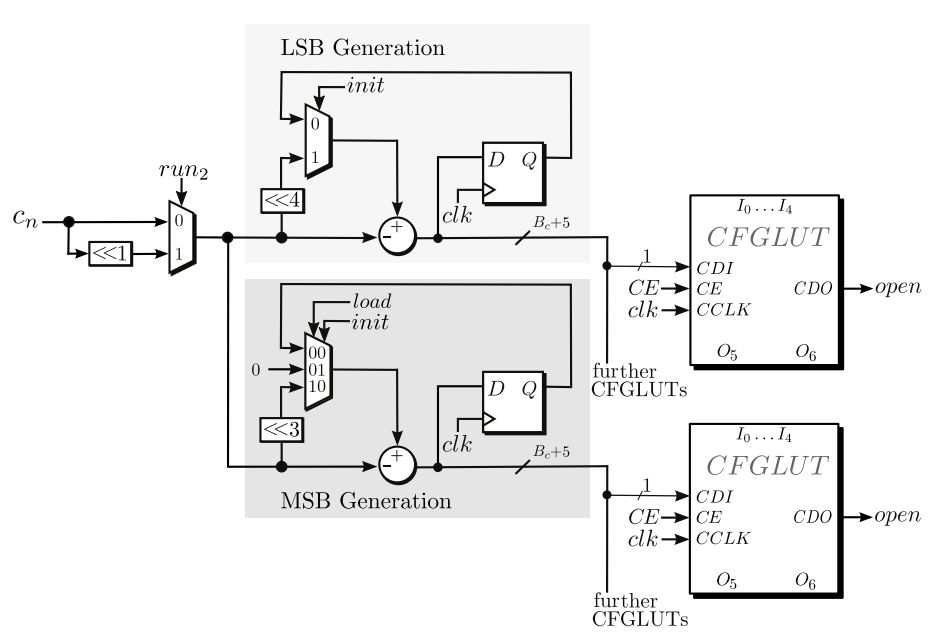
图4.3 动态配置LUT电路图

从上述架构中可以看到，当进行LUT配置的时候，LUT是无法进行计算的。这个很好解决，可以通过增加双倍LUT来实现，对没有计算的LUT来进行动态配置，而另一部分LUT进行计算。这样相当于进行了ping-pong操作。

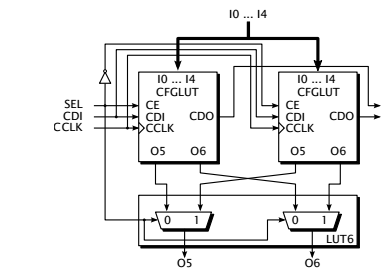
图4.4 双LUT结构进行计算

结果

下图给出了不同卷积核大小以及不同位宽所需要的资源对比。相比于其他使用LUT来进行乘法和加法操作的方式来说，这样更能最大化利用LUT资源。

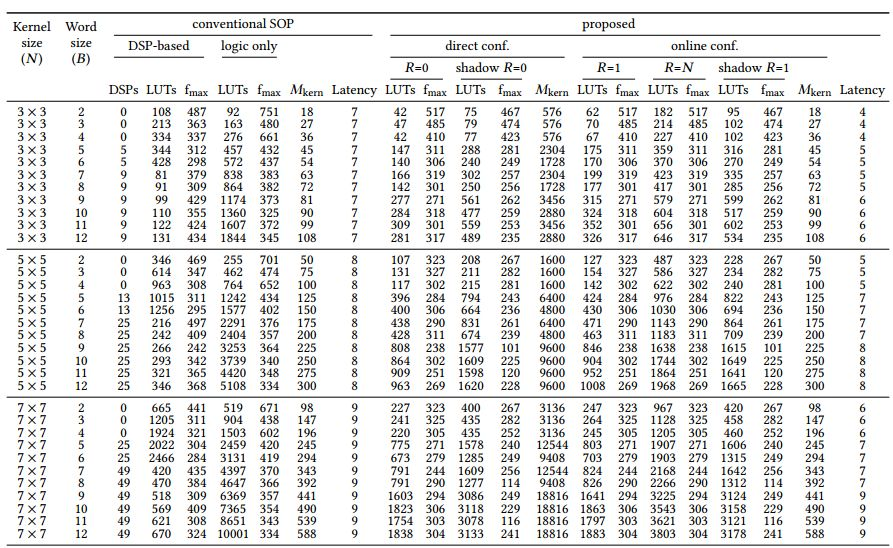
图5.1 综合后资源对比

总结

论文中提出的可配置卷积运算架构，可以改善CNN在FPGA的应用。充分利用了LUT资源，可以更好的改善时序性能。